Nonlinear MHD simulations of stellarator plasmas
The stellarator, one of the oldest magnetic fusion concepts, has received revived interests recently due to the successful construction and operation of the Wendelstein 7-X (W7-X) device. Stellarator plasmas generally have more favorable MHD stability than the more mainstream tokamaks, and in particular, are often found to be more robust than what linear stability theory predicts. I have extended the state-of-the-art M3D-C1 code to stellarator geometry to enable pioneering studies on such nonlinear stability, which could potentially expand operation windows for present devices and improve designs for future ones. Below are a few snapshots from a preliminary simulation of a sawtooth-like crash on W7-X induced by a small amount of electron-cyclotron current drive.

3D MHD equilibria with current singularities
Ideal MHD, in which the magnetic field is frozen into the fluid motion due to perfect conductivity, allows for solutions with singular current densities, the formation of which can have profound real-world consequences. In toroidal fusion plasmas, this concerns the existence of smooth 3D MHD equilibria with nested flux surfaces. In solar physics, this amounts to Parker’s theory of coronal heating, a long-standing conundrum, by so-called nanoflares. My results on current singularity formation are conclusive in periodic geometry (for toroidal fusion) while suggestive in line-tied geometry (for solar corona). Shown below is that the current density distribution becomes more concentrated as the length of the line-tied system increases, but whether the solution will be genuinely singular at a finite length remains an open problem.

Structure-preserving numerical methods
In computational physics, numerical schemes are desired to inherit conservation laws from the continuous systems. One approach to designing such schemes by preserving the structures that underpin the conservation laws, i.e., structure-preserving discretization, has become quite popular in plasma physics. In particular, structure-preserving particle-in-cell methods have matured and are ready to be used in production. For ideal MHD, I developed a moving-mesh variational integrator that is free of numerical resistivity, which facilitated the aforementioned studies on current singularity formation. Below is a demonstration of this feature by simulating the coalescence instability of magnetic islands, which would typically trigger artificial reconnection with conventional numerical methods. However, this fully Lagrangian method has a limited application domain, and more robust (semi-Lagrangian or Eulerian) structure-preserving discretization of MHD, and fluid systems in general, turns out to be much more challenging.
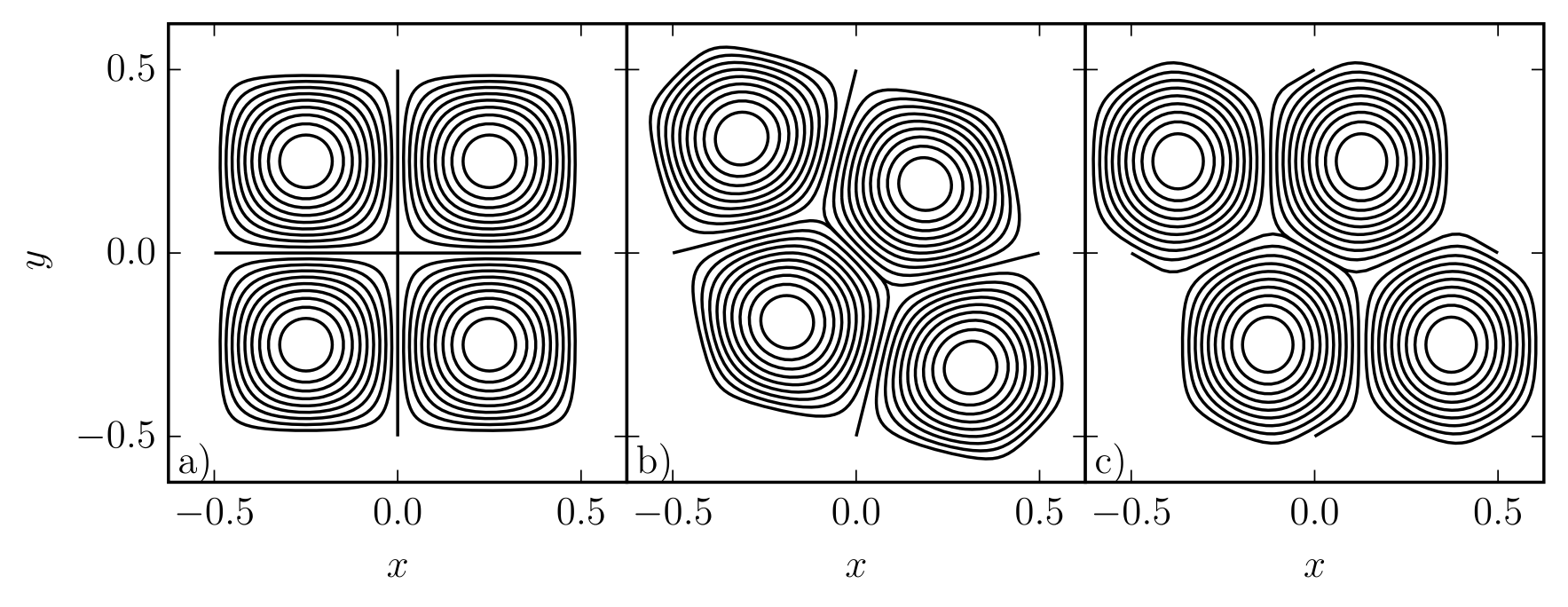
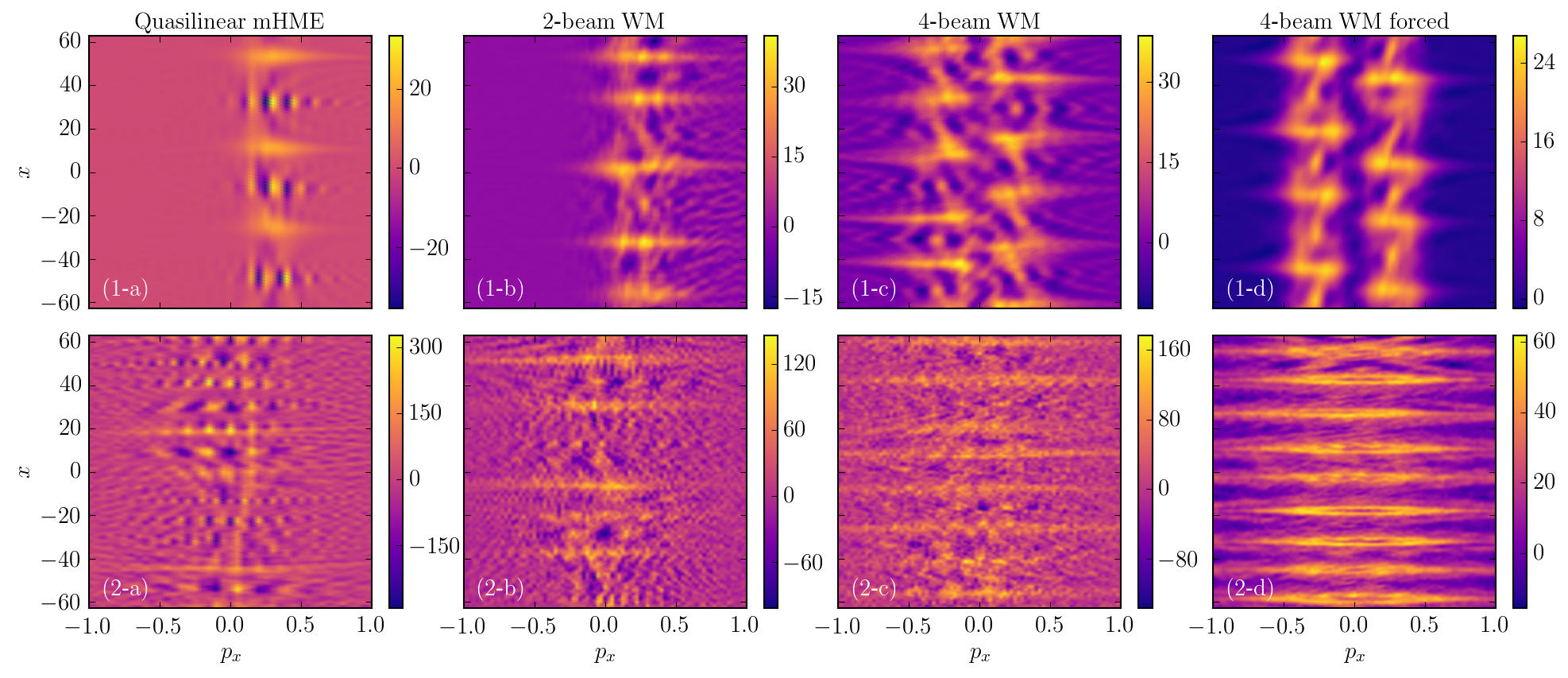
Wave turbulence and coherent structures
A powerful tool for studying inhomogeneous wave (e.g., drift or Rossby) turbulence is the wave-kinetic approach, which considers wave-packets as quasi-particles in phase space that interact via a collective field, much like a plasma. Traditional wave-kinetic theory assumes scale separation and adopts the ray approximation, but recently a more advanced Wigner-Moyal model has been proposed, which treats waves as quantum-like particles and retains essential “full-wave” effects. I implemented this model numerically and applied it to studying coherent structures in drift-wave turbulence. Below are snapshots of Wigner functions, which show intricate phase-space structures, of solitary (row 1) and stationary (row 2) zonal structures in various simulations.
Modern wave theory and ray tracing
An approach closely related to wave kinetics is ray tracing, a.k.a. geometrical optics, which is widely used in many areas such as computer graphics. In plasma physics, ray tracing is often used in modeling propagation of radio-frequency waves in magnetic fusion and laser beams in inertial fusion. However, there are scenarios where geometrical optics fails, such as caustics and mode conversions, which are actually quite important in practice. Thankfully, recent advances in modern wave theory may extend geometrical optics such that modeling them becomes possible. Shown below are Wigner fuctions of 1D full-wave simulations of the ordinary-extraodinary-Bernstein conversion in a magnetized plasma, which transparently visualize the process in phase space.

